Traffic
Description
Traffic is software application developed in order to study emergent forms based on the interaction between elementary objects. A large part of the motivation for these experiments was to create visual forms musically, an artform most commonly referred to as 'visual music.' Here, it is not only the 'what' that makes something musical, but more important the 'when.' Two musical concepts used in this exploration were the building of form from units and the arrangement of events over time. More specifically, these concepts refer to the construction of visual timbre using additive techniques to create forms from parts and visual rhythm by both positioning and movement over time of particles.The primary unit used in this study was a particle called a Rect (short for rectangle). A Rect has space-time, representational, and behavioral properties that determine its appearance and its interaction with other objects. A Rect is a representation for a two-dimensional, single-derivative space-time particle.
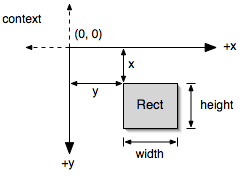
class Particle{
Particle(int numDimensions, int numDerivatives);
// Space-time attributes
int dimensions;
int derivatives;
float * d; // space-time derivatives (position, velocity, acceleration, etc.)
void update(); // compute position based on derivatives
}
class Rect : public Particle{
// Representational attributes
float width, height; // spatial dimensions
Color color; // rgba
// Behavioral attributes
int numCollisions;
float colorCharisma;
}
Study #1 - Collision Visualization
The first exploration involved devising different ways of visualizing the collisions between moving Rects on the screen. Mathematically speaking, a collision occurs whenever two Rects have a non-zero intersection. Observing these intersections was an attempt to accentuate the spatial relationships of a large group of Rects. Four modes of collision visualization were originally proposed and implemented.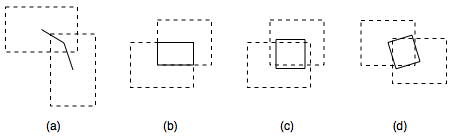
 |
 |
 |
 |
| Mode (a) | Mode (b) | Mode (c) | Mode (d) |
Visualizations (a) and (d) exhibited a visual "popping" since they had maximal spatial dimensions during initial and terminal contact of two Rects. Modes (b) and (c) had a smoother visual envelope since they depended on the area of the intersection.
Study #2a - Collision Interaction: Velocity Scaling
The next study explored how the Rects time-space property, velocity, could be modified based on spatial relationships with other Rects. The method devised was to scale the velocity of a Rect depending on whether or not it was colliding with another Rect. This required adding an additional velocity scaling factor to all Rects, so their original velocity could be preserved. For example, the old way of updating a position was like this:x = x + dx;The new way is like this:
x = x + dx * dxScale;Two complementary methods were used to modify the velocity scaling factor: (a) slow down when colliding and (b) slow down when not colliding. The following images show the two modes.
 |
 |
| (a) slow on collide | (b) slow on no collide |
Mode (a) produced clumps of Rects in certain locations where smaller velocity scaling factors resulted in longer lifetimes of the clumps. Mode (b) had the effect of dissolving clumps of Rects where smaller velocity scalings resulted in longer lifetimes of non-clumps, i.e. non-intersecting Rects.
Study #2b - Collision Interaction: Velocity Combining
To expand on the Rects spatial behavior over time, it was decided to combine the velocities of two intersecting Rects. The formula used in the experiment was a simple weighted-averaging of velocity based upon area.float ratio = rect1.area() / ( rect1.area() + rect2.area() ); float dxt = rect1.dx + rect2.dx; float dyt = rect1.dy + rect2.dy; rect1.dx = dxt * ratio; rect1.dy = dyt * ratio; rect2.dx = dxt * ( 1 - ratio ); rect2.dy = dyt * ( 1 - ratio );Combining velocities of Rects produced even more prominent clumping behavior than was seen with simple velocity scaling. The behavior over time was interesting, as the Rects exhibited a flocking like motion to higher density areas. The following images illustrate this.
 |
 |
| Velocity combining with Rects shown | Velocity combining without Rects shown (blurred to show motion) |
Study #2c - Collision Interaction: Color Combining
To further illustrate the interactions between Rects and produce emergent forms, color information was combined amongst the Rects. The technique to do this was very similar to how how the velocities were combined in the previous section. When a Rect is "born", it is assigned a color and a so-called color charisma value. The possible colors, red, green, blue, or grey are chosen based on a two-pass probability mechanism. First, a color probability vector is chosen at random, then a color is chosen from the vector based on its color probabilities.| p vector | p(red) | p(green) | p(blue) | p(grey) |
| 1 | 0.026 | 0.002 | 0.002 | 0.97 |
| 2 | 0.002 | 0.026 | 0.002 | 0.97 |
| 3 | 0.002 | 0.002 | 0.026 | 0.97 |
This color picking technique was chosen to avoid a kind of color frequency "noise" by restraining colors to a specfic hue.
When a new color is chosen for a Rect, a color charisma value is assigned to the Rect. The color charisma determines how much the Rect will influence other Rects' colors upon a collision. For this study, larger color charismas were assigned to non-grey colors and smaller values to grey colors. It was done this way so that color information can propagate more easily through the interactions between Rects.
Study #3 - User Controllability
This experiment was done in order to give more human control over the forms that were created. The most direct, and most tedious, mode of interaction allows you to click on individual Rects and drag them with the mouse. This was not found very useful since many Rects would have to be moved to make any significant changes. However, it was found useful to be able to see motion relative to a Rect by clicking on it. If a Rect was part of a moving group of Rects it could be clicked on to cause the group to become motionless. Another mode of interaction found useful was to attract/repel the Rects to/from the mouse cursor position. The following images show using repulsion and attraction from the mouse to warp the positions of the Rects on the screen. |
 |
| Repulsion | Attraction |
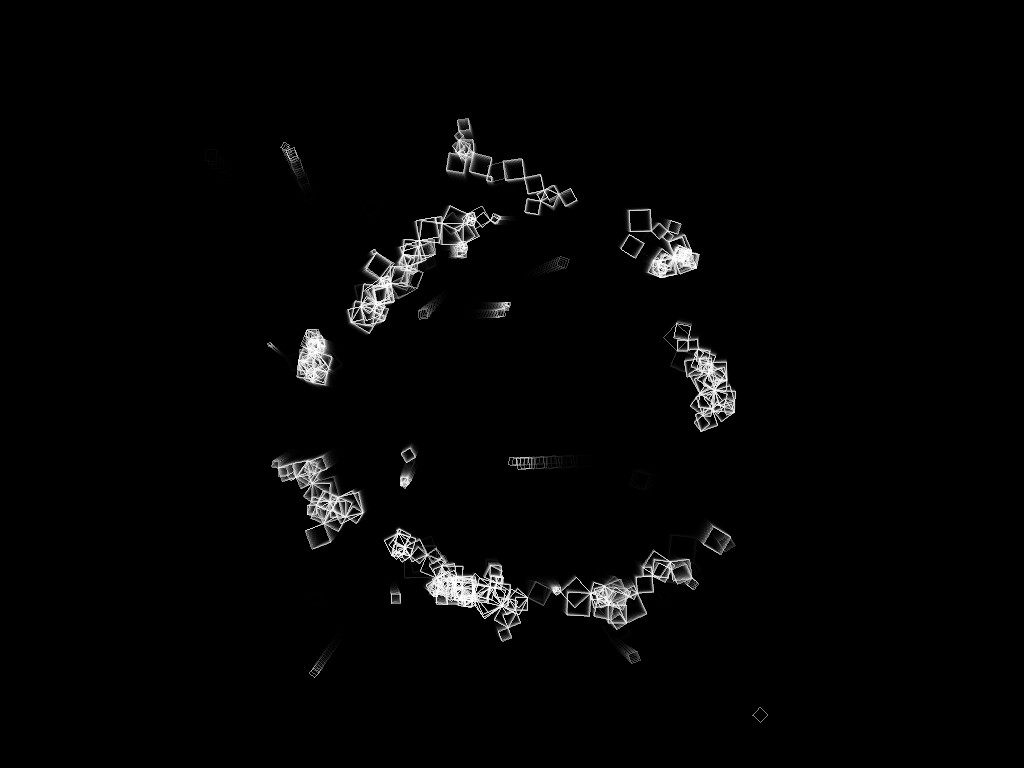
Study #4 - Initialization Presets
It quickly become evident that only a limited amount of interaction would be possible using the same algorithm to initialize the starting parameters of the Rects. For all of the above experiments, the Rects would be initialized to a random location on the edge of the screen with random velocities. This is shown as preset (a) in the following illustrations.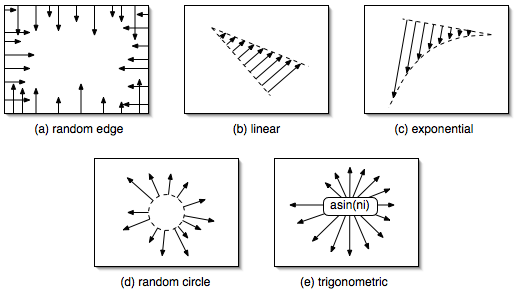
 |
 |
 |
 |
| (b) with Rects | (b) without Rects | (c) with Rects | (c) without Rects |
 |
 |
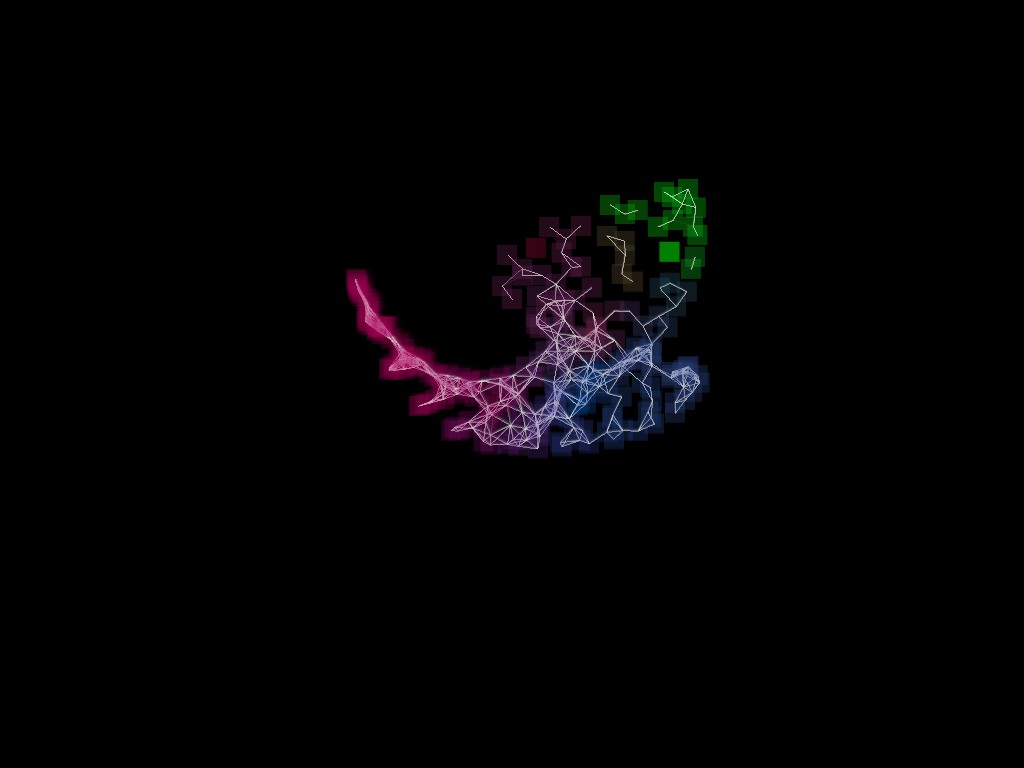 |
 |
| (d) with Rects | (d) without Rects | (e) with Rects | (e) without Rects |
Study #5 - Real Virtuality
The final area of exploration was to connect the digital world to the physical world. The idea was to use time as one of the spatial dimensions, so that a 3-d model could be built by stacking a sequence 2-d images. This was accomplished by using the medical imaging software OsiriX. OsiriX allows you to import raw data as 2-d image sequences that it then uses to create a 3-d model. The 3-d model can then be exported as one of several popular formats such as .obj and .stl. A Z-Corp 3-d printer was then used to print a physical object based on the exported .stl file from OsiriX. The following are images of a 3-d printed object made using preset (e) from Study #4. |
 |
 |
| 3-d model "harp" | Inner striae | Moire-like patterns on outside |
The smaller end of the object was the start of time and the bottom, where the shape spreads out, is the end of time. Interesting striations and Moire-like patterns were generated from the movement of the Rect corners over time.