Turtlets
These are a selection of line drawings made with very basic turtle graphics algorithms. The algorithms describe how the turtle should update its position and orientation on successive iterations. The basic structure in code is:
for(int i=0; i<20000; i++){
move(expression 1);
turn(expression 2);
}
where
move(x) | moves turtle forward x units |
turn(x) | turns turtle x degrees |
i | iteration number |
rng.uniform() | returns a uniform random number in [0,1] |
rng.uniformS() | returns a uniform random number in [-1,1] |
rng.prob(x) | returns true with a probability of x |
While randomness generally produces pleasing results, I find that non-random algorithms often produce more interesting structure. Randomness produces figures with a satisfying "spread", however, the overall structure is typically very uniform and lacks sufficient variety at micro- and macro-scales. The most satisfying patterns seem to lie on the border of predictability and unpredictability. With randomness, it is easy to produce unpredictable results, but difficult to produce repeating and symmetrical patterns.
Spiral A
move(1); turn(i*12.34567);

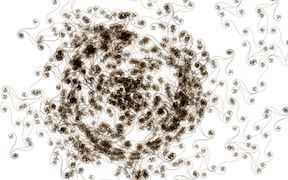
Spiral B
move(1); turn(i*1.001);


Spiral C
move(1); turn(i*14.001);


Ornament A
move(1); turn(i*7030307 % 36 + 11);
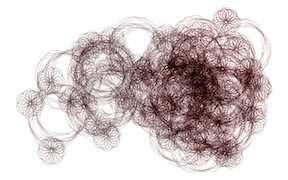
Ornament H
move(1); turn(i*12345678 % 360);


Bug Pray
move(1); turn(i*846728391 % 360);

Biostrand A
move(1); turn(i*84622839 % 36);
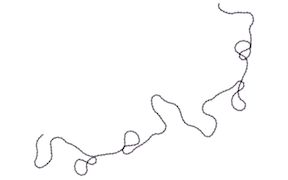

Biostrand B
move(1); turn(i*84622839 % 44);


Biostrand C
move(1); turn(i*6906713 % 36);

Biosystem A
move(1); turn(i*9015109 % 36 + 17);
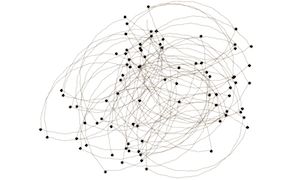

Spiro A
move(1); turn(i*i*179 % 36 + 5);


Spiro B
move(1); turn(i*i*193 % 36 + 5);


Scribbles
move(1); turn(rng.uniform()*36);



Twigs
move(1); turn(rng.prob(0.9) ? 179 : 10);



Random Walk
move(1); turn(rng.uniform()*360);



Random Pentagonal Walk
move(1); turn(rng.uniform(5)*72);



Random Walk on Defective Grid
move(1); turn(rng.uniform(4)*90 + 0.1);



Square Walk
move(1); turn(rng.prob(0.9) ? 89 : 10);

Furry Walk
move(1); turn(rng.uniformS()*10 + 180);



Patterns In Chaos C
move(1); turn(i*i*414640 % 20);


Patterns In Chaos D
move(1); turn(i*i*414650 % 20);

